Source: http://www.math.tamu.edu/~sottile/research/stories/4triangles/index.html

H. Brönnimann, O. Devillers, S. Lazard, i F. Sottile

Razmotrimo sljedeće jednostavno geometrijsko pitanje: Koji je maksimalni broj linija koje su tangentne na četiri trokuta? (To jest, brojimo linije koje zadovoljavaju jedan rub svakog trokuta.) Radi jednostavnosti, pretpostavljamo da su trokuti u prikladnom općem položaju, u tome što algebarsko opuštanje gdje zamjenjujemo rubove potpornim linijama ima samo konačan broj rješenja. (Zapravo 162 različita složena rješenja.)

Tražimo maksimalni mogući broj, jer je minimum nula: ako su četiri trokuta dovoljno udaljena, recimo na četiri ugla vrlo velike prostorije, tada neće biti takvih uobičajenih transverzala.

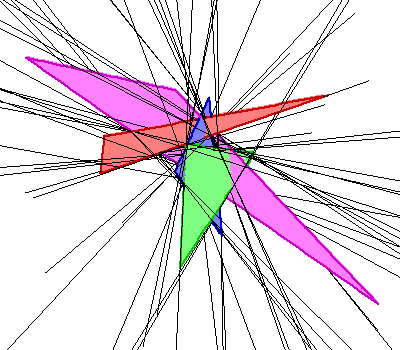
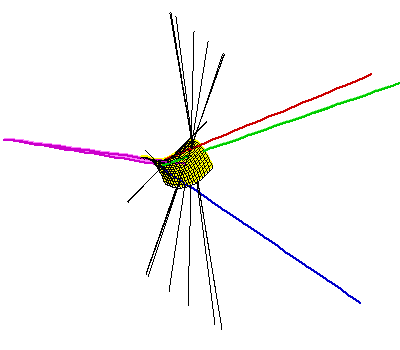
Trenutno je najbolji odgovor na ovo pitanje da je maksimalni broj između 62 i 162, s gornjom granicom od 156 ako su trokuti nepovezani. Gornja granica gotovo sigurno nije najbolja moguća, a također sumnjamo u optimalnost donje granice. Ova donja granica je posljedica konstrukcije koju opisujemo na ovoj stranici (povezana s donjom slikom desno). Ova konstrukcija uključuje uznemiravanje četiri segmentna pravca koji imaju 2 zajednička transverzala, a svaki od rezultirajućih trokuta ima jedan izuzetno mali kut – vrlo su tanki. Naša najbolja konstrukcija koja uključuje četiri masna trokuta ima 40 zajedničkih transverzala. Opis pretraživanja računala pomoću kojeg smo pronašli ovaj primjer povezan je s slikom na lijevoj strani ispod, kao i animacijama.

Ova stranica WWW prati naš rad na tu temu, O broju linija tangente na četiri trokuta u trodimenzionalnom prostoru.
Slike su povezani s daljnju raspravu

Na temelju rada koji je podržala Nacionalna zaklada za znanost pod CAREER Grant DMS-0134860.

Napisano: 30. prosinca 2004. Frank Sottile