Source: http://urila.tripod.com/Osmosis_Carnot.htm

Uri Lachish, zadržati znanost

Priča počinje u Parizu, Slavoluk pobjede i aveniji Elizejske poljane. Kao što znamo, put počinje od Slavoluka pobjede, ali ne samo ovaj put. Postoji više cesta koje počinju odatle prema svim smjerovima. Koliko? Bio sam tamo i izbrojao dvanaest. Jedan od njih je avenija Carnot. Tko je bio Carnot? Lazare Carnot (1754.-1823.) Bio je general u Napoleonovoj vojsci, a kasnije i ministar u svojoj vladi. Nakon Napoleonova poraza otišao je u izgnanstvo i nikad se više nije vratio. On je također bio izvanredan matematičar. Zašto smo zainteresirani za njega? Zapravo, nismo stvarno zainteresirani, čak ni uopće. Zanima nas njegov sin Sadi Carnot (1796. – 1832.). Tu je i put u njegovu čast negdje drugdje u Parizu. Sadi nije tipično francusko ime, već ime perzijskog pjesnika.

Sadi Carnot je živio u prvoj polovici 19. stoljeća. Bio je inženjer koji je radio za francusku vojsku i bavio se najnaprednijom tehnologijom tog vremena. Koja je tada bila tehnologija? – Parni motori.

Danas su parni strojevi nostalgija, “chif chif chaf je lokomotiva napuhnuta”, ali stvari su se tada vrlo razlikovale. Ako ste htjeli otići iz grada u grad, umjesto da sjedite u kočiji, skočite na kamenje, potonite u blato i budite ranjivi na autoceste, umjesto svega toga, uskoro će biti moguće ići na vagonu i udobno stići na vrijeme do odredišta. Ako, primjerice, želite ploviti u daleku zemlju, umjesto da putujete jedrilicom i zaglavite tjednima u središtu oceana jer nema vjetra, umjesto da ćete uskoro putovati s parobrodom i znati kada odete i kada stignete. Možda je najvažnije da će se u gradove moći pumpaju vode, a ne treba ih donositi iz bunara ili rijeke s vrčevima, što je vrlo romantično, ali ne i zgodno.

Budućnost je izgledala obećavajuće, izgledala je sjajno, a naš Carnot je tražio načine kako poboljšati parni stroj. Ono što mu se tada dogodilo je ono što se dogodilo kralju Saulu u njegovo vrijeme. Šaul je otišao potražiti magarce i pronašao kraljevstvo. Carnot je otišao tražiti parne strojeve i što je pronašao? Otkrio je najvažniji zakon znanosti oduvijek. Danas se ovaj zakon naziva drugim zakonom termodinamike.

Uskoro ćemo govoriti o pravu Carnota, ali prije nekoliko riječi o čovjeku. Sadi Carnot preminuo je u ranoj dobi, u tridesetim godinama, u jednoj od pošasti koja je tada bila moderna, i nije znao da je takav čovjek. Vjerojatno i mi ne bismo znali, a ni nitko drugi, da nije drugi čovjek otkrio zakon 30 godina kasnije. Ovaj čovjek nije bio samo veliki znanstvenik, nego i velik čovjek i zato ćemo ga poštovati i zvati ga po imenu Clausius. Za razliku od onoga što je danas uobičajeno, ljudi uzimaju posao drugih i pripisuju ga sebi, nakon što je otkrio zakon, Clausius je otišao i sjeo u knjižnice i pogledao u stare arhive, da vidi je li netko drugi otkrio zakon pred sobom. Na kraju je pronašao Carnotovo djelo, objavio ga i dao mu sve zasluge i poštovanje. Zašto je Carnotov zakon drugi zakon termodinamike? Jer je tijekom 30 godina koje su prošle prvi zakon otkriven. Danas se to zove očuvanje energije.

Nakon tako pompoznog uvoda moglo bi se pomisliti da je najmanje 10 godina na sveučilištu potrebno naučiti Carnotov zakon, ali to uopće nije tako. Svijet Carnota bio je dinamičan svijet procesa – kotači, klipovi koji se penju gore-dolje, ventili koji se otvaraju i zatvaraju, parna zvižduka kroz dimnjake, tohooo…, a Carnot je pokušao razmišljati o tim procesima na apstraktniji način. Posebno ga zanimaju “reverzibilni procesi”.

Što je reverzibilni proces? Kao i njegovo ime, moguće je preokrenuti smjer njegova rada. Najbolje je vidjeti primjer kao na sljedećoj slici gdje vidimo istezanje gumene vrpce. Držanje trake na određenoj dužini zahtijeva specifičnu silu istezanja između ruku. Ako se sada sila malo poveća, pojas će se malo više rastegnuti, a ako se sila smanji na prethodnu vrijednost, traka će se skratiti na prethodnu duljinu. Ova vježba se ponavlja za različite duljine, a ovdje je reverzibilan proces. Jasno, ako se bend sve više rasteže, na kraju će se nepovratno rastrgati. Dakle, proces je reverzibilan samo unutar određenog raspona duljine pojasa.

Slika 1: Ispruženi gumeni pojas – primjer reverzibilnog procesa. Povećanje sile će produljiti traku. Smanjivanje sile na prethodnu vrijednost skratit će traku na njezinu prethodnu duljinu.

Nisu svi procesi reverzibilni, primjerice miješajući žlicu punu šećera u čajnoj šalici. Šećer se nakon toga ne može “pomiješati” s čajem tako da se promijeni kretanje žlice. Miješanje šećera je nepovratan proces.

Carnot je pretpostavio da su reverzibilni procesi najučinkovitiji u prirodi. Svaki proces koji nije povratan bit će manje učinkovit. Ovaj jednostavan postulat ima, kao što ćemo vidjeti, dalekosežne posljedice, a Carnot ga je koristio za analizu rada parnog stroja. Rad parnog stroja je složen proces koji uključuje korake grijanja i hlađenja, a Carnot se morao baviti punim ciklusom rada, neki od njih s povećanjem ili smanjenjem temperature. Naš sustav desalinizacije je jednostavniji i moguće je pretpostaviti da je temperatura jednolika i konstantna.

Sada, da smo opremljeni ovim snažnim zakonom Carnota, vrijeme je da pređemo na desalinizaciju vode. Slika 2 prikazuje posudu izgrađenu od U oblika cijevi s polupropusnom membranom na svom dnu koja razdvaja svoje dvije ruke. Polupropusna membrana je membrana koja omogućuje prolaz vode kroz nju, ali blokira prolaz soli.

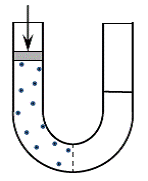
Slika 2: Polupropusna membrana razdvaja krakove U oblika cijevi koja sadrži vodu. Sol u lijevoj ruci u njoj stvara osmotski tlak. Pritisak na klip iznad otopine na lijevoj ruci određuje smjer protoka vode kroz membranu.

Voda se najprije dodaje u posudu i budući da može prolaziti s jedne strane na drugu, doseći će istu razinu na obje ruke. Sada, neka sol je dodana u lijevu ruku. Sol koja ne može proći u drugu ruku otapa se u vodi i stvara osmotski tlak koji inducira protok vode iz ruke čiste vode u ruku otopine soli. Vodeni prolaz podiže razinu otopine iznad razine čiste vode. Ovaj proces prolaska vode zove se osmoza. Zašto se stvara osmotski tlak? I zašto izaziva prolaz vode? Namjerno ćemo ta pitanja zadržati na kasnijoj raspravi.

Moguće je zaustaviti prolaz vode iz ruke u ruku stavljanjem klipa na lice otopine i stvaranjem pritiska na njega koji je jednak osmotskom tlaku. Sada je sustav u statičnom stanju, ništa se ne pomiče. Ako povećamo pritisak na klip, on će se pomaknuti prema dolje i voda će se vratiti iz otopine soli u čistu vodu. To je reverzna osmoza, a proces je desaliniziranje jer smo prenijeli vodu iz otopine soli u čistu vodu. Ako smanjimo tlak na klipu natrag na početnu vrijednost, smjer protoka vode će se opet preokrenuti, voda će proći u otopinu soli i klip će se pomaknuti prema gore i vratiti u početni položaj. Što je taj proces? Točno, to je reverzibilni proces. Što nam Carnotov zakon govori o tome? To je vjerojatno djelotvorno.

Kada klip potisne volumen V vode kroz membranu, obavljeni rad jednak je osmotskom tlaku koji je ovaj volumen. Tako da znamo koliko energije treba uložiti kako bi se desalinizirala određena količina vode. Ta energija je minimalna potrebna za desalinizaciju jer je proces reverzibilan. U bilo kojem drugom procesu koji nije povratan morat ćemo uložiti više energije.

Uložena energija u guranje klipa prema dolje jednaka je energiji koja se vraća kada se klip vraća u prvobitni položaj. Ovaj se opis čini previše dobrim da bi bio istinit i doista postoje gubici tijekom svake faze koji se ne mogu izbjeći. Na primjer, prolaz vode kroz membranu uključuje neizbježan gubitak energije koji ne ovisi o smjeru protoka vode. Guranje klipa zahtijeva više energije nego reverzibilna granica, a kada se povuče unatrag, dobiva se manje energije nego što se postiže reverzibilna granica. Energija je izgubljena u oba smjera. To je moguće samo smanjiti smanjivanjem brzine protoka vode. Stoga je reverzibilni proces apstrakcija ili granica prirodnog procesa koji uvijek uključuje ireverzibilni gubitak.

Iz ovih razmatranja jasno je da nije moguće desalinizirati vodu bez ulaganja energije. Ako bismo na neki čarobni način uspjeli desalinirati vodu iz otopine bez ikakvog unosa energije, mogli bismo uzeti tu vodu i proizvoditi energiju s našim plovilom vraćajući vodu u otopinu soli s procesom osmoze. Ponavljanjem ove procedure dobivamo perpetuum mobilni stroj koji proizvodi energiju iz ničega. Takav proces, naravno, nije moguć.

Kao srednji sažetak, postoji proces osmoze i reverzne osmoze o kojem gotovo ništa ne znamo, ali uz pomoć Carnotovog zakona znamo o njemu puno.

Prije Carnota pogled na materijalni svijet bio je utemeljen na mehanici Newtonovih zakona. Newtonovi zakoni su deterministički. Prema njima, ako je poznato stanje sustava, tj. Položaj i brzina svih čestica u sustavu, tada zakoni točno određuju mjesta gdje će čestice biti u bilo kojem trenutku u budućnosti. Slično tome, zakoni određuju mjesta i brzine gdje su bili u bilo kojem trenutku u prošlosti. Zapravo, znanje, ne znajući, nije toliko važno. Zakoni ionako djeluju na čestice. Ovaj deterministički pogled na svijet, koji je u suprotnosti s našim svakodnevnim iskustvom, dugo je vremena bila velika zagonetka.

Mehanički pogled na svijet naveo je ljude da traže detalje pojedinih sustava kako bi na njih primijenili Newtonove zakone i razumjeli ih na taj način – i više detalja – to bolje. Nasuprot tome, upotreba Carnotovog zakona u našem skromnom primjeru osmoze omogućuje razumijevanje važnih pitanja u sustavu s kojim gotovo i nismo upoznati i koje ne razumijemo. U mnogim slučajevima, detaljno znanje, koje je potrebno u mehaničkom pogledu, nije potrebno. Carnotov zakon proširuje ideju o tome što je znanost. Ako se prije Carnota samo matematika, fizika, astronomija, a možda i malo kemije, smatrale znanostima, Carnotov zakon otvorio je široka vrata za proučavanje znanosti o životu, ekonomiji i društvenim znanostima, kao i umjetnosti i humanističkih znanosti. O sustavima se može raspravljati smisleno čak i ako se o njima zna vrlo malo.

Naizgled naivni postulat Carnota, da će proces koji nije reverzibilan uvijek biti manje učinkovit od reverzibilnog procesa, ima još važnije implikacije. Pretpostavimo da snimamo proces koji nije video s kamerom. U nekom trenutku zastajemo i pokrećemo film unatrag, kao što smo vidjeli mnogo puta na televiziji ili u filmovima. Je li zaostali film, koji gledamo, mogući proces u prirodi? Prema Newtonu, da. Sve što trebamo učiniti je zaustaviti sustav i preokrenuti smjer svih čestica unatrag. Sve će se čestice vratiti u početna mjesta i sustav će se vratiti u početno stanje, kao što se vidi u obrnutom filmu. Što o tome govori Carnotov zakon? Nikako. Zašto? Jer, ako je učinkovitost prvobitno snimljenog procesa ispod razine reverzibilnog procesa, tada će učinkovitost procesa u nazadnom procesu, koji vraća sustav u početno stanje, biti viši od onog u reverzibilnom procesu. To u prirodi nije moguće u skladu s Carnotovim zakonom. Tko je u pravu? Newton ili Carnot? Stvarnost nam govori da je Carnot u pravu. Newtonovi zakoni nisu u stanju razlikovati prošlost i budućnost. Nasuprot tome, ovo svojstvo Carnotovog zakona, da nije moguće obrnuti procese u prirodi unatrag, znači da postoji razlika između prošlosti i budućnosti. Stoga u Carnotovom zakonu postoji nešto novo što ne postoji u Newtonovim zakonima. Trebalo je dugo da se ovo pitanje shvati.

Pionirski rad Carnota, neki kažu “prosvjetljenje”, doveo je put do znanosti o termodinamici. Sposobnost bavljenja sustavima kada se o njima ne zna mnogo, dovela je do uvođenja vjerojatnosti u teoriju, a iz toga u znanost o mehanici statistike. Kvantna teorija, razvijena tijekom prve polovice 20. stoljeća, zamijenjena “ne zna” po “ne može znati” i time je sukob s determinističkim Newtonovim zakonima u velikoj mjeri nestao. Termodinamika i statistička mehanika od tada su ušle u temelj svih grana znanosti i bez njih se čini nemogućim. Na primjer, “crne rupe”, ta čudna tijela u svemiru koja apsorbiraju sve što im je u blizini. Termodinamički argumenti posljednjih godina ukazuju da i ta tijela sporo isparavaju i gube svoj materijal dok ne nestanu.

Nakon lutanja na takvim visinama, vrijeme je da se sleti na čvrstu zemlju i vrati se desalinizaciji vode. Možemo se sjetiti kilo-kalorija iz školskih dana, energetske jedinice koja je jednaka količini topline potrebne za zagrijavanje litre vode za jedan stupanj Celzijusa. Da bismo zagrijali jednu litru od temperature od 20 stupnjeva do temperature vrenja od 100 stupnjeva, trebamo, dakle, 80 kilograma kalorija. Ako želimo prokuhati ovu vodu i pretvoriti je iz tekućine u paru, trebat će nam još 540 kilograma. Koliko kilo-kalorija je potrebno za desalinizaciju jedne litre morske vode? Minimalna energija, prema Carnotovom zakonu, je nešto više od pola kilograma. U postrojenjima za desalinizaciju postoje neizbježni gubici, a stvarno potrebna energija je oko 2 do 3 kilograma. Čak i tako, energija potrebna za zagrijavanje vode za šalicu kave daleko je veća od energije potrebne za desalinizaciju ove vode.

Desalinizacija bez sumnje zahtijeva energiju, ali zasigurno nije energetski intenzivna, a budući da na mnogim mjestima u svijetu postoji veliki nedostatak vode, to će postati samo još ozbiljnije, ali ne postoji drugi način da se to primjeni. Voda za grijanje je mnogo energetski intenzivnija. Tijekom šezdesetih godina prošlog stoljeća donesen je zakon kojim je svaki novi stan morao imati solarni bojler. Tijekom godina zakon je rezultirao značajnom uštedom goriva i energije. Bilo bi zanimljivo znati koliko je od tada bilo spašeno.

Neka mjesta, poput Skandinavije i Sibira, imaju višak čiste vode. Na tim mjestima moguće je proizvesti energiju osmozom iz slanosti morske vode. Poseban slučaj je mrtvo more koje je desetak puta veće od morske. Desetljećima se voda rijeke Jordana ispumpavala iz Galilejskog jezera i koristila za piće i navodnjavanje. Ako bi se dopustilo da se riječna voda ponovno izlijeva u Mrtvo more, kao u prošlosti, tada bi bilo moguće proizvesti energiju tamo gdje se rijeka ulijeva u more. Može se proizvesti mnogo više energije jer je voda mnogo više slane. Postrojenje za desalinizaciju u punoj veličini može pružiti sličnu količinu vode i istovremeno se Mrtvo more može spasiti od isparavanja i na kraju nestati.

Postoji još jedan dug. Što je zapravo osmoza?

Objašnjenje fenomena osmoze dao je Vant-Hoff, nizozemski kemičar, i on mu je osvojio prvu Noble nagradu u kemiji 1901. godine. i pretpostavlja se da je formula osmotskog tlaka u otopini identična s tlačnom formulom idealnog plina u spremniku. Analogija zaključuje da osmotski tlak ne ovisi o tipu otopljenih čestica, već je proporcionalan njihovoj koncentraciji.

Van’t-Hoff piše: “Mehanizam kojim se, prema našim sadašnjim konceptima, proizvodi elastični tlak plinova, u suštini je isti kao i onaj koji uzrokuje osmotski tlak u otopinama. utjecaj molekula plina na zid posude, u posljednjem, na utjecaj molekula otopljene tvari na polupropusnu membranu, budući da su molekule otapala prisutne na obje strane membrane kroz koje se prolaz, ne ulazite u obzir. ”

Van’t-Hoff je također prvi predložio prostornu trodimenzionalnu strukturu kemijske molekule, te je tim prijedlogom otvorio nove horizonte znanosti o kemiji i svemu što slijedi. U povijesnoj perspektivi ovaj rad može vrijediti i Nobelove nagrade. Van’t-Hoff pomislio je na trodimenzionalnu strukturu dok je bio student doktorskog studija, ali netko ga je savjetovao da ga ne objavljuje odmah, već da pričeka i podnese standardniji posao za taj stupanj, i tako je i učinio.

Srećom za van’t-Hoff, eksperimentalni podaci o osmozi nisu bili dovoljno jasni, pa je mogao proći svoju teoriju. Uskoro je otkriveno da formula osmotskog tlaka djeluje u molekulama poput šećera, ali čak is jednostavnom molekulom kao što je stolna sol osmotski je tlak oko dvostruko veći od izračunatog iz formule.

Ovakav rezultat doveo je do toga da švedski kemičar Arrhenius sugerira da se molekula kuhinjske soli raspada na ione natrija i klora kada se otopi u vodi. Budući da se svaka molekula soli sastoji od tih dvaju iona, njihova ukupna koncentracija je dvostruka koncentracija molekulske koncentracije. Stoga se osmotski tlak također treba udvostručiti. Arrhenius nije primio savjet sličan onome koji je dao van’t-Hoffu, i podnio je tu teoriju za svog doktora znanosti. Njegovi profesori nisu mu vjerovali, ali su se bojali diskvalificirati njegov rad. Tako su mu dali nisku prolaznu ocjenu. Arrhenius je postao poznat s predstojećim godinama, pridonio važnijim znanstvenim dostignućima, a 1903. dobio je Nobelovu nagradu.

Van’t-hoffova analogija između osmotskog tlaka i tlaka plina nije prihvaćena s godinama koje su uslijedile. Mnogi protivnici su je odbacili, a to se i danas ne prihvaća. Bilo je i jesu ljudi koji tvrde da je sličnost između osmotskog tlaka i tlaka plina samo slučajnost. O ovoj temi nema mnogo koristi, a preostaje samo navesti neke od najvećih znanstvenika.

Mladi i još ne poznati čovjek, Albert Einstein, patentni istraživač trećeg stupnja u patentnom uredu u Bernu, napisao je 1905. godine pet znanstvenih radova koji su promijenili svijet, a ove godine je postao poznat kao “annus mirabilis” – godina čuda, Njegov drugi rad bavi se “Brownovskim pokretom”. Brown je bio botaničar koji je kroz mikroskop gledao sitne čestice koje lebde u kapi vode. Čestice nisu bile u mirovanju, nego su stalno vibrirale i pomicale se s mjesta na mjesto na slučajan način. Isprva se taj fenomen pripisivao živim tijelima, ali se tada ispostavilo da je to opaženo u neživim česticama. Einstein je taj fenomen objasnio tako što je predložio da ga tekuće molekule, koje okružuju česticu, neprestano udaraju iz svih smjerova i time ih prisiljavaju da se kreće nasumce.

Zašto je ovo objašnjenje važno? Svi znaju da su materijali sastavljeni od atoma koji su se nekada smatrali osnovnim nedjeljivim česticama. Danas znamo da se atom sastoji od jezgre od protona i neutrona koja je okružena elektronima. Ove čestice su izgrađene od još temeljnijih čestica. Tijekom 19. stoljeća nije se uzimala zdravo za gotovo, a mnogi su smatrali da atomi zapravo ne postoje, već su samo matematička pogodnost koja pomaže u izvođenju proračuna. Nakon objavljivanja Einsteinovog djela, ideja da stvarno postoje atomi postala je općeprihvaćena.

Na početku svog rada Einstein piše (izvor je na njemačkom): “Moramo pretpostaviti da suspendirane čestice izvode nepravilan pokret – čak i ako je vrlo spor – u tekućini, zbog molekularnog kretanja tekućine; ako ih se spriječi da napuste volumen V* preko particije, oni će vršiti pritisak na pregradu baš kao molekule u otopini.” [3]. (pregrada je polupropusna membrana).

Enrico Fermi, jedan od važnih sudionika razvoja kvantne teorije i nuklearne fizike, koji je također izgradio prvi nuklearni reaktor, napisao je knjigu pod nazivom “Termodinamika”. Knjiga je dobila pohvale za njegovu dubinu razmišljanja i jasnoću izlaganja, a čini se da je vrlo malo njih čita. Evo kratkog odlomka iz rasprave o osmozi: “Tada će se pritisak na strani membrane koja je okrenuta prema otopini povećati utjecajem na nju molekula otopljenih tvari” [4].

Citati govore sami za sebe. Pisac ovih stranica smatra da je osmotski tlak bitan za održavanje ravnoteže linearnog momenta na rješenju. To je manje-više ono što kažu Einstein i Fermi.

Zašto molekule vode mogu prodrijeti kroz polupropusnu membranu? Pisac je tražio objašnjenje, ali ga nije pronašao. On pretpostavlja da propusna membrana sadrži hidrofilna mjesta koja privlače vodu, a molekule vode hitaju od mjesta do mjesta i na taj način prolaze kroz membranu.

Ukratko, razmišljanja o značenju znanosti, znanosti i svijetu mogu doći od “velikog praska” i “božje čestice”, kao i od pitanja vodovoda.

Reference:

1. S. Carnot, „Osvrt na pogonske snage vatra”, Dover Publications, Inc., New York (1960, 1988)
2. J.H. van’t Hoff, „Uloga osmotskog tlaka u analogiji između otopina i plinova”, Časopis za fizičku kemiju, svezak 1, str. 481-508 (1887)
   J.H. van’t Hoff, „Funkciji osmotski tlak u analogija između rješenja i plinovima„,
   preveo W. Ramsay, Filozofski časopis, S. 5. svezak 26. br 159. kolovoz, str. 81-105 (1888)
   J.H. van’t Hoff, „Uloga osmotski tlak u analogija između rješenja i plinovima„,
   u: Suvremena teorijska rješenja, memoari po Pfeffer, van’t Hoff, Arrhenius i Raoult,
   preveo i uredio Harry C. Jones, Harper & Brothers Publishers, New Yorku i Londonu, str . 11-42
3. A. Einstein, „Na prijedlog malih čestica suspendiranih u tekućinama u mirovanju koja je potrebna za molekularnu-kinetička teorija topline„, izvorno objavljen u Anali fizike 17 [1905]: 549-560
   A. Einstein, „ Istraživanja na teoriji od Brownovog kretanja„, u prijevodu A.D. Cowper, Dover Publications, Inc., New York, str. 1-18 (1956)
4. E. Fermi, „Termodinamika”, Dover Publications, Inc., New York (1936, 1957), str. 118-123

Na internetu: prosinac 2012. godine.

Autor:

1. Osmoza desalinizaciju Carnot, http://urila.tripod.com/Osmosis_Carnot.htm, prosinac (2012).
2. „Svjetlo rasipanja”, http://urila.tripod.com/scatter.htm, kolovoz (2011).
3. „Sunce i Mjesec zagonetku na nebu”, http://urila.tripod.com/moon.htm srpnja (2011).
4. „Osmoze i termodinamika”, Američki časopis za fiziku, svezak 75 (11), str. 997-998, studeni (2007).
5. „Van’t Hoff dokazi”, http://urila.tripod.com/evidence.htm, listopad (2007).
6. „Osmoze i termodinamika”, http://urila.tripod.com/osmotic.htm, siječanj (2007).
7. „Proširenje idealnog plina”, http://urila.tripod.com/expand.htm, prosinac (2002).
8. „Optimiziranje učinkovitosti reverzne osmoze morske vode desalinizaciju”, http://urila.tripod.com/Seawater.htm svibnja (2002).
9. „Boltzmann transport jednadžbi”, http://urila.tripod.com/Boltzmann.htm, svibanj (2002.).
10. „Energetska morske vode desalinizaciju”, http://urila.tripod.com/desalination.htm, travanj (2000).
11. „Avogadrov broj atomska i molekularna masa”, http://urila.tripod.com/mole.htm, travanj (2000).
12. „Tlak pare, vrenja i niske temperature otopine”, http://urila.tripod.com/colligative.htm, prosinac (1998).
13. „Osmoza obrnute osmoze i osmotski tlak što su” http://urila.tripod.com/index.htm, veljača (1998).
14. „Proračun linearnih koeficijenata u ireverzibilnih procesa pomoću kinetičkih argumentima”, Američki časopis za fiziku, svezak 46 (11), str. 1163-1164, studeni (1978).
15. „Izvođenje nekih osnovnih svojstava idealne plinove i rješenja iz procesa elastičnih sudara”, Časopis za kemijsko obrazovanje, svezak 55 (6), str. 369-371, lipanj (1978).

Linkovi:

1. Termodinamika istraživački laboratorij, http://www.uic.edu/~mansoori/Thermodynamics.Educational.Sites_html
2. Termodinamika – toplo nastava, http://www.schulphysik.de/thermodyn.html
3. Slijepci i slon
4. Moj Spin na ludilo
5. Pet tjedana u balonu
6. Prvi čovjek sam vidio
7. „Brže, brže!”
8. Savršenstvo ne može biti jurnu
9. Čovjek viši
10. Mozak
11. Prve klase putnika
12. drugo